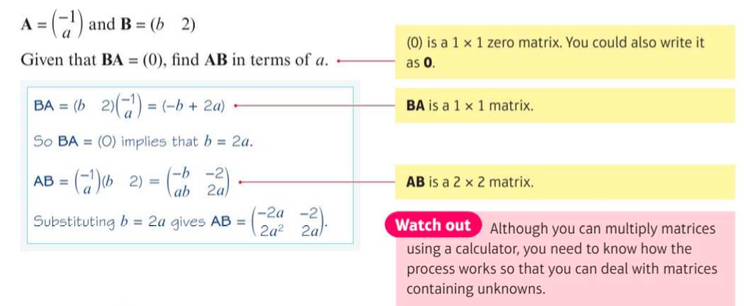
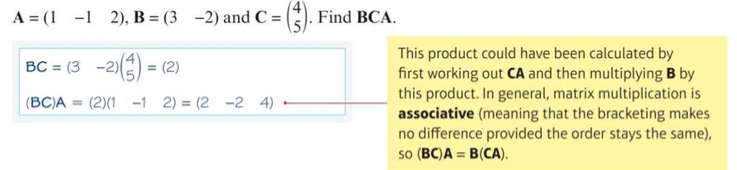
Matrix Multiplication
Introduction
⇒ Two different matrices cn be multiplied together. Unlike the operations we have seen so far, this is completely different from normal arithmetic multiplication
⇒ Matrices can be multiplied together if the number of columns in the first matrix is equal to the number of rows in the second matrix
- If AB exists, then matrix A is said to be multiplicatively conformable with matrix B
⇒ The product matrix will have the same number of rows as the first matrix, and the same number of columns as the second matrix
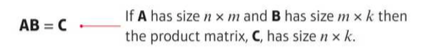
⇒ The order in which you multiply matrices is important. This has two consequences:
- In general AB ≠ BA (even if A and B are both square matrices)
- If AB exists, BA does not necessarily exist (for example if A is a 3 x 2 matrix and B is a 2 x 4 matrix)
- To find the product of two multiplicatively conforamble matrices, you multiply the elements in each rown in the left hand matrix by the corresponding element in each column in the right hand matrix, then add the results together

Examples